R ile Korelasyon, Regresyon ve Zaman Serisi Analizleri
KORELASYON
Korelasyon rassal iki değişken arasındaki doğrusal ilişkinin gücünü ve yönünü ifade eder.
Bu konuda R ile bir çalışma yapalım. R’a yerleşik olarak gelen mtcars veri setini kullanarak korelasyon matrisi oluşturup bir takım uygulamalar gerçekleştirelim:
mtcars, 1973-1974 model 32 aracın yakıt tüketimi, dizayn ve performans ölçülerini içeren bir data setidir. Detay için ?mtcars yazabilirsiniz.
summary(mtcars) head(mtcars) # mpg: Mil/Galon # cyl: Silindir sayısı # disp Silindir Hacmi # hp: Toplam Beygir Gücü # drat: Arka Aks Oranı # wt: Ağırlık (lb/1000) # qsec 1/4 mil zamanı # vs: V/S # am: Vites Türü (0 = otomatik, 1 = Manuel) # gear: İleri vites sayısı # carb: Karbürator sayısı
Korelasyon matrisi nedir?
Korelasyon matrisi çoklu değişkenler arasındaki korelasyon katsayılarının tablosudur. Bu tabloda bir değişkenin diğer her değişken ile arasındaki korelasyon görülebilir.
Korelasyon matrisi oluşturalım:
korelasyon_matris <- cor(mtcars)
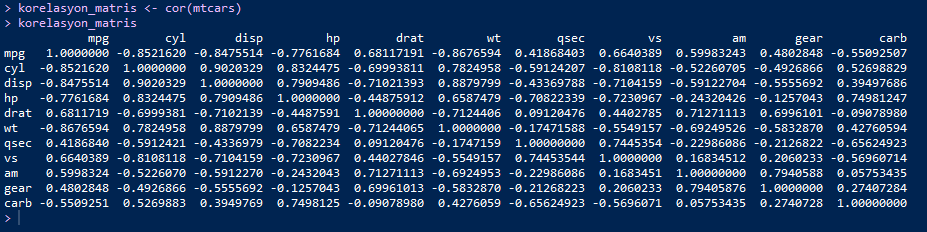
Elde etmiş olduğumuz korelasyon katsayılarını corrplot paketi ile görselleştirerek daha yalın bir şekilde görelim:
# install.packages("corrplot")
library(corrplot)
corrplot(korelasyon_matris, method = "circle")
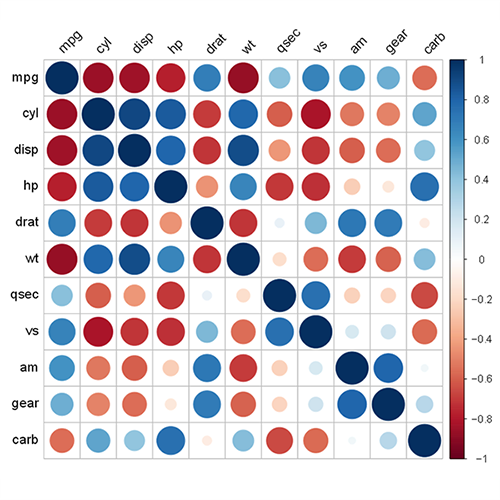
Bu grafik ile tüm değişkenlerin birbirine bağlılık derecesini daha net bir şekilde gördük. Grafik üzerindeki koyu mavi noktalar güçlü pozitif korelasyonları, koyu kırmızı noktalar ise güçlü negatif korelasyonları göstermektedir. Diğer daireler de renklerine ve büyüklüklerine göre korelasyonun gücünü ve yönünü belirtmektedir.
Şimdi korelasyon katsayılarını ifade eden bu daireleri gruplayalım ve zayıf korelasyonları çıkaralım. Yardım için ??corplot yazıp ilgili dökümanı inceleyebilirsiniz.
cor.mtest <- function(mat, conf.level = 0.95) {
mat <- as.matrix(mat)
n <- ncol(mat)
p.mat <- lowCI.mat <- uppCI.mat <- matrix(NA, n, n)
diag(p.mat) <- 0
diag(lowCI.mat) <- diag(uppCI.mat) <- 1
for (i in 1:(n - 1)) {
for (j in (i + 1):n) {
tmp <- cor.test(mat[, i], mat[, j], conf.level = conf.level)
p.mat[i, j] <- p.mat[j, i] <- tmp$p.value
lowCI.mat[i, j] <- lowCI.mat[j, i] <- tmp$conf.int[1]
uppCI.mat[i, j] <- uppCI.mat[j, i] <- tmp$conf.int[2]
}
}
return(list(p.mat, lowCI.mat, uppCI.mat))
}
res <- cor.mtest(mtcars, 0.95)
corrplot(korelasyon_matris, method = "circle", order = "hclust", p.mat = res[[1]], sig.level = 0.05, addrect = 2, tl.col="black", tl.srt=45)
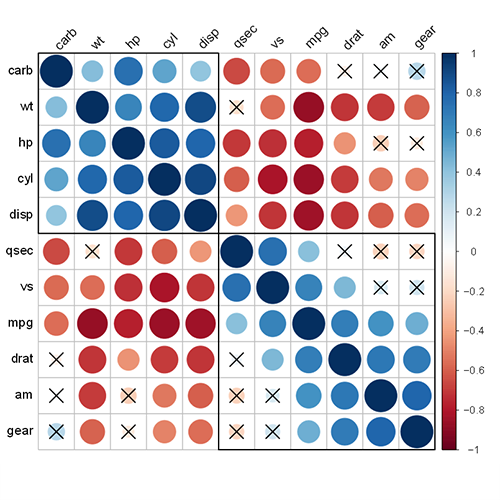
Şu halde, güçlü pozitif korelasyonlar bir köşegen üzerinde, negatif korelasyonlar da diğer köşegen üzerinde toplandı. Zayıf korelasyonları ifade eden dairelerin üzeri çizildi.
Sahte Korelasyonlar
Bu gibi bir çalışmalarda pek çok sahte korelasyon çıkabilir. Sahte korelasyon, neredeyse birbiri ile hiçbir nedensellik bulunamayacak iki değişken arasında güçlü bir korelasyon çıkması durumudur.
Örneğin:
Bir ülkedeki çikolata tüketimi ile o ülkedeki insanların kazandığı toplam nobel ödülü sayısı arasında pozitif bir korelasyon var.
Internet Explorer kullanım oranı ile suç oranı arasında pozitif bir korelasyon var.
ABD’nin Maine eyaletindeki boşanma oranı ile kişi başına düşen margarin tüketimi arasında güçlü bir pozitif bir korelasyon var. (0,99)
Bunun için şu ayrıntıyı her zaman akılda tutmakta fayda var: Korelasyon nedensellik değildir.
REGRESYON
Regresyon da iki ya da daha çok değişken arasındaki ilişkiyi ölçmek için kullanılan bir analizdir. Biri bağımlı biri bağımsız olan iki değişkenin fonksiyonel ifadesidir.
Aynı şekilde R ile bir takım çalışmalar yapalım:
Yine mtcars data setini kullanalım:
# sınıfı numerik olan cyl sütununu factor sınıfına dönüştürelim. mtcars$cyl
Şimdi bir grafiği oluşturalım:
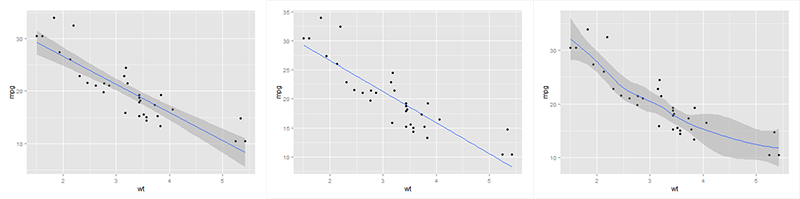
#install.packages(“ggplot2”) library(ggplot2) ggplot(mtcars, aes(x=wt, y=mpg)) + geom_point(size=4, color="blue", shape=20)
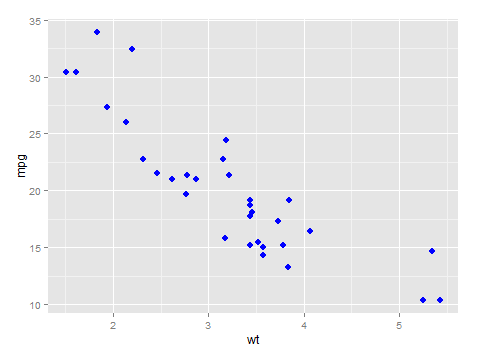 Bu ilişkiyi ifade eden regresyon doğrularını ekleyelim:
Bu ilişkiyi ifade eden regresyon doğrularını ekleyelim:
# Regresyon doğrusu eklemek ggplot(mtcars, aes(x=wt, y=mpg)) + geom_point()+ geom_smooth(method=lm) # Güven aralığı kaldırıldığında ggplot(mtcars, aes(x=wt, y=mpg)) + geom_point()+ geom_smooth(method=lm, se=FALSE) # Loess metodu ggplot(mtcars, aes(x=wt, y=mpg)) + geom_point()+ geom_smooth()
ZAMAN SERİLERİ VE TEKNİK ANALİZ
Zaman serileri bir zaman aralığı içinde ölçülen veri serisidir. Zaman seri analizleri için R oldukça faydalı bir araçtır.
Hisse senetleri ve benzeri piyasalarda analiz yapmak için çok kullanışlı bir paket olan quantmod’u inceleyelim:
Apple Inc. şirketinin 1 Ocak 2015 tarihinden bu yazının yazıldığı güne kadarki günlük fiyat değişimini görelim (01.01.2015 – 10.10.2015) :
#install.packages("quantmod")
library(quantmod)
getSymbols("AAPL") # Apple Inc. Hissesi, Yahoo Finance
apple_hisse <- AAPL["2015-01-01::2015-10-10"] # 1 Ocak 2015 tarihinden bu yazının yazıldığı güne kadar
chartSeries(apple_hisse, type="candlesticks") #Apple Inc. Hisse Senedi Grafiği
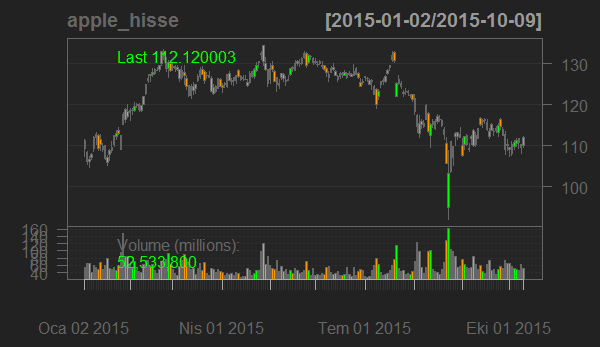
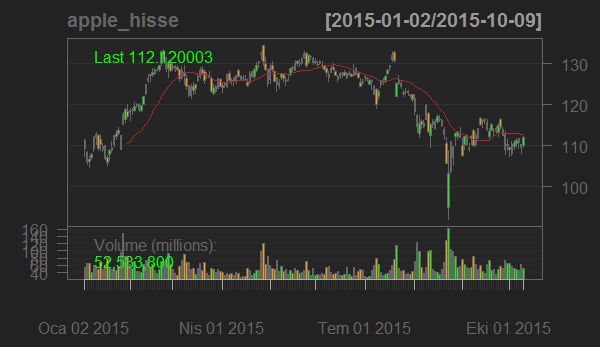
R ile Apple Inc. şirketinin hisse senedini pek çok modern platformdaki gibi inceleme imkanımız var. Şimdi bu hisse senedinin trendini gözlemlemek için bir Basit Hareketli Ortalama ekleyelim. Bu hareketli ortalama ile fiyat hareketlerini yumuşatarak trend hakkında bir fikir sahibi olabiliriz. (Aşağıdaki grafik üzerindeki kırmızı eğri).
addSMA(20) #20 günlük bir basit hareketli ortalama
Ve son olarak trendin gücü hakkında fikir sahibi olabileceğimiz Relative Strength Index osilatorünü ekleyelim:
addRSI(14) # Relative Strength Index
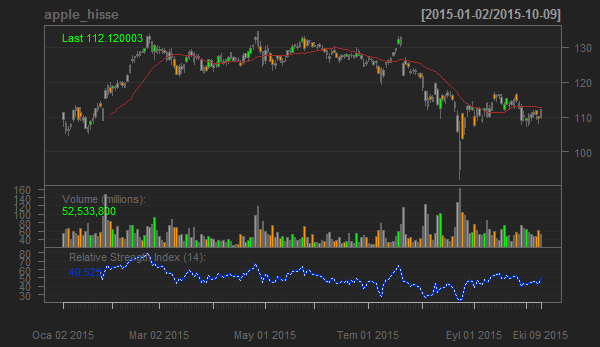
Teknik Analiz konusu altında incelenen pek çok indikatör ve yöntem quandmod paketi içinde gelmektedir. R, bu ve benzeri analizler için pek çok platformda bulabileceğiniz analiz yöntemlerinden çok daha büyük imkanlar sunabilmektedir.
Finans ve araştırma konularında R ile ilgili kaynaklar için: http://www.opiyasa.com/kategori/istatistik-arastirma/
Data Driven Kavramı ve II. Faz Daha İyi Bir Veri Bilimcisi Olmanız İçin 5 İnanılmaz Yol
Çok güzel bir çalışma olmuş teşekkür ederim:)
Merhaba. Güzel bir çalışma olmuş. Ellerinize sağlık.
Gerçekten çok faydalı bir çalışma. Paylaşımınızdan dolayı teşekkür ederim.