Basit Lineer Regresyon
Basit lineer regresyon, 2 nicel veri arasındaki ilişkiyi özetleyen istatiksel bir metoddur. X ekseninde gösterilen 1.değişken tahmin edici, bağımsız değişkendir. Y ekseninde gösterilen 2.değişken ise tahmin edilen çıktı ise bağımlı değişkendir.
Basit lineer regresyon ile bulunan bu ilişki, istatistiksel bir ilişkidir. Bu bağlamda istatistiksel ve deterministik ilişkiden bahsedelim.
Deterministik ilişki, 2 değişken arasındaki ilişkiyi kesin olarak tanımlayan bi denklem mevcuttur. Örneğin;
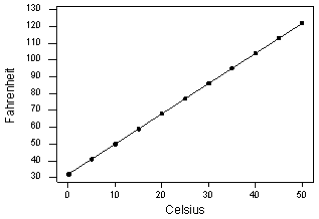 Fahrenheit ve Celcius arasındaki ilişkisi kesin olarak gösteren bir denklem vardır ve grafikte görüldüğü gibi her Celcius’a karşılık gelen değer kesin denklem sonucu çıkan kesin değerdir.
Fahrenheit ve Celcius arasındaki ilişkisi kesin olarak gösteren bir denklem vardır ve grafikte görüldüğü gibi her Celcius’a karşılık gelen değer kesin denklem sonucu çıkan kesin değerdir.
Fahr = 95Cels+32
İstatistiksel ilişki ise değişkenler arasındaki kesin olmayan ilişkiyi tanımlar. Örneğin, boy uzadıkça doğru orantılı olarak kilonun da artması beklenir ama bu her zaman doğru değildir. Çünkü bu sonucu etkileyen birden fazla durum vardır biz sadece 1 tane durumu alarak sonuç üretmeye çalışıyoruz. Bütün durumlarla çalışmasında bile kesin sonuç üretilmez.
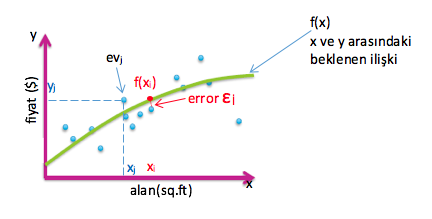
Regresyon konusu boyunca ev fiyat tahminlemesi örneği üzerinden ilerleyeceğiz. Elimizde evlere ait evin fiyatı, alanı, banyo sayısı, bahçe alanı vs gibi özellikler mevcut, bu özelliklere veri setimize dahil olan evin fiyat tahminlemesini yapacağız. Konumuz Basit Lineer Regresyon olduğu için 2 değişkenimiz olacak, evin fiyatı ($) ve alanı(sq.ft). Evin alanı (bağımsız değişken) x ekseninde, evin fiyatı (bağımlı değişken) y ekseninde yer alacaktır.
Veri setimizde ki evler, evi = (xi,yi) olarak tanımlanır. Regresyonla oluşan model, evin tahminlenen fiyatına (f(x) fonkisyonu) gerçek fiyattan tahminlenen fiyatın çıkarılması ile bulunan değerin (hata) eklenmesi ile bulunan;
Regresyon model:
yi = f(xi) + εi
Hatanın 0 olması istenilen durumdur, hatanın pozitif yada negatif olması verinin eğrinin üstünde yada altnda kalmasına göre değişir.
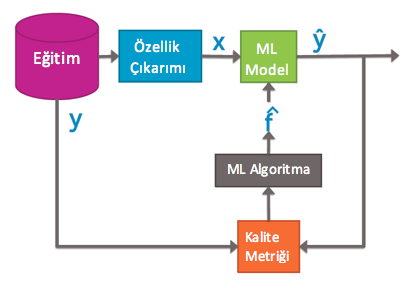
Veri üzerinde Regresyon nasıl çalışır?
Örneğimizde yola çıkarak şema üzerinden ilerleyelim. Eğitim verisi, yazının başında bahsettiğim gibi evlere ait belirli değerlerdir. Özellik çıkarımında modelde oluştururken kullanacağımız x ,evin alanı. Regresyonla oluşan Model’in (f) sonucu tahmin edilen fiyat y kalite metriği olan evin gerçek fiyatı y ile karşılaştırılarak hata (error) bulunur. Hataya göre model güncellenir.
Basit regresyon sonucunda oluşan lineer doğru f(x) = w0 + w1 x , oluşan model ise yi = w0 + w1 xi + εi dir. w0 ve w1 regresyon katsayıları olan intercept ve slope dur. Veriye uygun olan model nasıl bulunur, yada modelin uygun olma kriteri nedir ? Bunun için uygun doğrunun bulunması gereklidir.
Uygun doğru nedir?
Uygun doğru, veri en yakın şekilde tahminleyen dolayısıyla hatanın az olduğu doğrudur. Bu kavramı öğrencilere ait boy ve kilo bilgilerinden oluşturulmuş örnek üzerinde irdeleyelim.
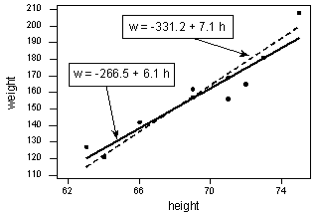
Örnekte 10 tane öğrenciye ait olan veriye 2 tane doğru uydurulmuştur, beraberce hangi doğrunun daha uygun olduğunu bulalım.
Doğru için kullandığımız denklem yi = w0 + w1 xi + εi idi. Şimdi doğru denklemlerinde öğrenciye ait boy bilgisini h yerine koyup, kilo yani tahminlenen w bilgisini elde edeceğiz. Elimizde bu öğrencilere ait gerçek kilo bilgileride yer aldığı için işlemleri yapıp 2 doğrudan hangisinde daha az hata varsa o doğruyu seçeceğiz. 1.öğrencinin boyu 63 inch, kilosu ise 127 pounds, doğruda bilgileri yerine koyduğumuzda;
w = -266.53 + 6.1376h
= -266.53 + 6.1376(63)
= 120.1 pounds
εi = 127- 120.1
= 6.9 pounds
Her bir doğru için her öğrenci bilgileri ile hata bulunur, hataların karesi alınarak toplanır. 1.doğrunun hata karelerinin toplamı ve 2. doğrunun hata karelerinin toplamı bulunur. İşlem sonucunda ;
w = -331.2 + 7.1 h ε1 = 766.5
w = -266.53 + 6.1376 h ε2 = 597.4
Hesaplamalara göre 2.doğrunun hatası daha küçük olduğu için uygun olan doğru 2.doğrudur. Hataların neden direkt toplanması yerine karelerinin alındığını düşünüyor olabilirsiniz. Bunun nedeni negatif ve pozitif hata oranlarının toplanırken birbirlerini götürmesini engellemektir.
Yukarıda her bir doğru için yaptığımız hata hesabı RSS olarak tanımlanır,
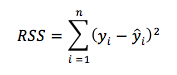 Intercept (doğrunun y ekseninde kestiği nokta) ve slope (eğim) üzerinden yazarsak aynı denklemi,
Intercept (doğrunun y ekseninde kestiği nokta) ve slope (eğim) üzerinden yazarsak aynı denklemi,
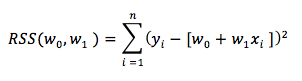 Sonuç olarak uygun doğru bulunurken doğrulara ait RSS değeri bulunur ve minimum RSS’e ait doğru, en iyi doğrudur.
Sonuç olarak uygun doğru bulunurken doğrulara ait RSS değeri bulunur ve minimum RSS’e ait doğru, en iyi doğrudur.
Model’in ve Doğru’nun incelenmesi
Model, bilinmeyen parametrelerden oluşturulan genel bir denklem iken, doğru ise tahmin edilen intercept ve slope ile yazılan spesifik bir denklemdir.
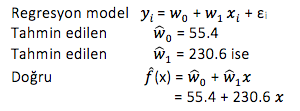 w0 > 0 ise yani slope (eğim) pozitif ise grafik te pozitiftir, x arttığında y nin de artacağı manasına gelir.
w0 > 0 ise yani slope (eğim) pozitif ise grafik te pozitiftir, x arttığında y nin de artacağı manasına gelir.
w0 < 0 ise yani slope (eğim) negatif ise grafikte negatiftir, x arttığında y nin de azalacağı manasına gelir.
Öğrencilerin boy ve kilo bilgilerinden oluşturulan doğruda xi = 0 ise
yi = -266.53 + 6.1376 xi
yi = -266.53
Bu değer boyu 0 inç olan bir öğrencinin kilosunun -266.53 çıktığı anlamına gelir ve manasız bir sonuç olur. Bunun nedeni x’in aralığıdır. (the scope of the model). Ayrıca xi = 0 modelinde iyi bir model olmadığını söyler bize, verinin gürültülü bir veri olduğu sonucuna bizi ulaştırır.
Intercept w^1 ise x ekseninde 1 birimlik değişimin y ekseninde ki karşılığı manasına gelir. Örneğin 66 inç ve 67 inç lik 2 kişinin kiloları tahmin edildiğinde 144.38 – 138.24 = 6.14 pounds bulunur, bu da 1 inç in 6.14 pounds değişimi ifade ettiğini anlatır. Fakat bu model oluşturulurken kullanılan birimler ile tahmin değerleri aynı ise bu yaklaşım doğrudur.
Least Square Optimizasyonu
Veriye en uygun doğruyu bulmak için w0 ve w1 değerlerinin minimum tahmin ederek dolayısıyla RSS i de minimum sağlamış oluruz. Pekala w0 ve w1 değerlerinin minimum değerlerini nasıl buluruz?
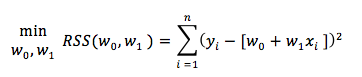
Öncelikle genel olarak fonksiyonlarda minimum ve maksimum nokta nasıl bulunur bakalım. Eğer fonksiyon iç bükey (concave) ise maksimum nokta bulmak için fonksiyonun türevi 0 eşitlenirken, dış bükey (conxex) ise minimum nokta bulmak için fonksiyonun türevi 0 eşitlenir.

Hill climbing: İç bükey fonksiyonlarda maksimum noktayı bulmak için kullanılan iterative bir algoritmadır. Eğrinin herhangi bir yerinden başlayarak ilerlediğimiz noktayı sağa yada sola doğru kaydırır. Sağa yada sola doğru kayacağımızı fonksiyonun türevinden anlarız. Eğer türev pozitif ise sağa doğru w yi artırarak ilerleriz, negatif ise sola doğru w yi azaltrak ilerleriz. Her attığımız adımla fonksiyonun türevi küçülmeye başlar bu da optimum noktaya yaklaştığımız anlamına gelir. Türev yeteri kadar küçüldüğünde max noktaya ulaşırız ve w u artırmayı bırakırız.
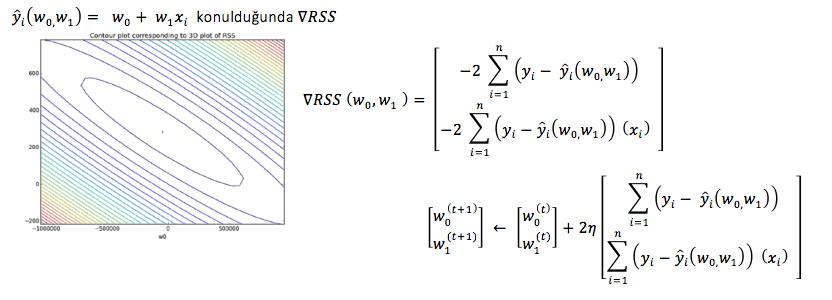
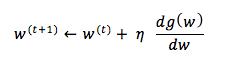 t iterasyonundaki değerler kullanılarak n adım boyu ile t+1 deki değer bulunur.
t iterasyonundaki değerler kullanılarak n adım boyu ile t+1 deki değer bulunur.
Hill descent : dış bükey fonksiyonlarda minimum nokta noktayı bulmak için kullanılan iterative bir algoritmadır. Hill climbing algoritması gibi, eğrinin bir yerinden başlayarak sağa yada sola doğru ilerlenir. Sağa yada sola doğru ilerleyeceğimizi fonksiyonun türevi üzerinden anlarız. Türev negatif ise sağa ilerleyip w yi artırıyoruz, pozitif ise sola doğru w yi azaltarak ilerliyoruz.
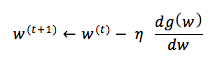
Adım boyu seçimi önemli bir konudur 2 algoritma içinde.
- Sabit adım boyu ile ilerlendiğinde minimum yada maksimum noktaya ulaşmak zaman alabilir.
- Adım boyunun azaltıralarak ilerlenilmesi ise daha çok tercih edilen bir yöntemdir.
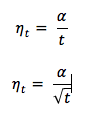
Adım boyumuz da belli fakat türevin 0 a eşit olduğu optimum noktayı bulamadık, ne zaman durmalıyız. Bunun için bir eşik değeri () belirlenir. Fonksiyonun türevi eşik değerinden küçük olduğunda ilerlemeyi durduruz ve o noktayı optimum nokta olarak kabul ederiz.
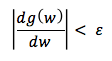
Gradients hesaplanması
Basit lineer regresyonda çalıştığımız fonksiyonlar 2 bilinmeyenli denklemlerdi (w0 ve w1). Çoklu değişkenler yüksek boyutta olduğundan türev yerine gradient hesaplaması yapılır. Gradient, her bir değişkenin kısmı türevinin yer aldığı vectordür. İterative olarak ilerlenilerek optimum nokta bulunur ve nokta bulunurken durulması gereken iterasyon yine bir eşik değeri ile sınırlayarak belirlenir.
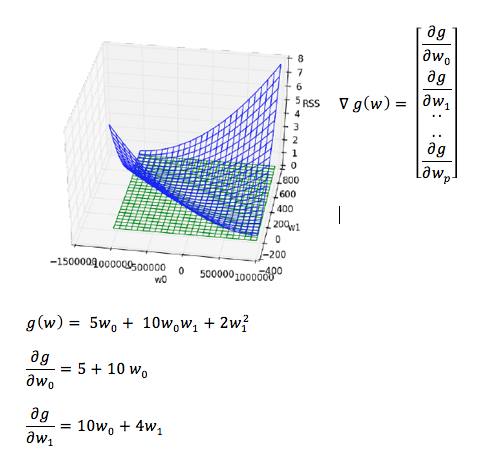 p tane değişkenli bir fonksiyondan p+1 lik bir vectör oluşur. Vectörün her bir elemanı değişkenlerin kısmı türevidir. Sonuç olarak w0 ve w1 değişkenli fonksiyonun gradient’i bulunur.
p tane değişkenli bir fonksiyondan p+1 lik bir vectör oluşur. Vectörün her bir elemanı değişkenlerin kısmı türevidir. Sonuç olarak w0 ve w1 değişkenli fonksiyonun gradient’i bulunur.
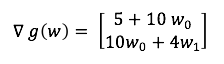
Gradient descent ise optimum noktayı bulmak için her adımda azalar ilerlemektir. Yine duracağımız nokta eşik değeri ile belirlenir.
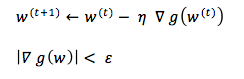
Least Square Doğrunun Bulunması
Veriye çizilen bir çok eğriden en uygun olanını seçmek için minimum RSS bulacağız, bunun için RSS ‘in gradientini hesaplamamız gerekmektedir. Örnekte convex bir fonksiyon üzerinden işlemler gerçekleştirilmektedir. Bulacağımız minimum değeri eşsiz (unique) tir ve gradient descent algortiması bu değere yakınsar.



Closed Form Çözümü
Bulunan Gradient’in 0 a eşitlenerek çözülmesi.
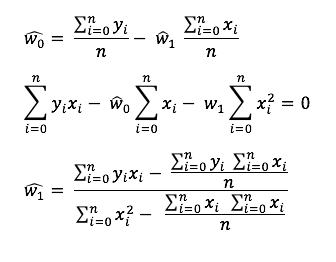
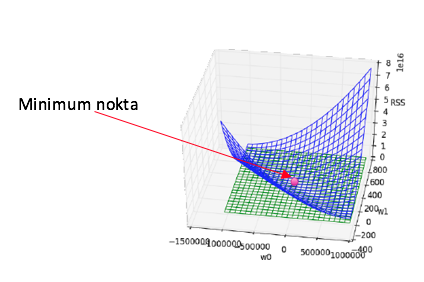
Gradient Descent Çözümü
Tek değişkenli denklemlerde ki hill descent algoritmasının çoklu değişkenli versiyonudur. Yandaki şekil gradient kuş bakışı görünümüdür ve her bir halka aynı fonkiyona aittir. Bir önceki adımdaki değerleri kullanarak bir sonraki değer elde edilir. RSS ‘in gradient hesabında tahmin yerine
2 Yöntemin Karşılaştırılması
Çoğunlukla tercih edilen yöntem Gradient Descent’tir fakat adım boyu, eşik değeri gibi durumları belirlemek zordur. Closed form da bu tarz belirlemeler olmadığı için daha kolaydır ama değişkenler arttıkça Gradient Descent’ti kullanmak daha verimli olur.
Örnekler:
Kaynaklar:
- Machine Learning, Tom Mitchell, McGraw Hill
- Introduction to Linear Algebra, Fourth Edition 4th Edition, Gilbert Strang
- https://www.coursera.org/learn/ml-regression/home/welcome
- https://onlinecourses.science.psu.edu/stat501/
Apache Sentry ile Yetkilendirme Hive Veritabanları Arası Tablo Taşıma
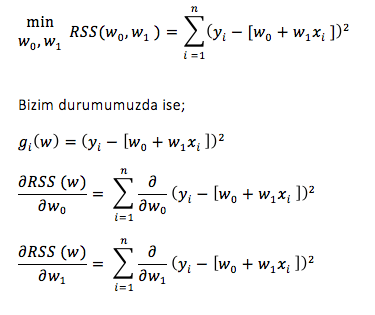
Gerçekten çok güzel, açıklayıcı bir anlatım. Böyle Türkçe kaynaklara çok ihtiyaç var. Emeğinize sağlık..
Yazılarınızın devamını bekliyorum. İyi çalışmalar..
oha çok iyi.
Çok teşekkür ederiz
anlam karmaşası yaratabilecek yerlerde virgül kullanmanız anlatımı daha kolay anlaşılabilir kılacaktır diye düşünüyorum
“Regresyonla oluşan Model’in (f) sonucu tahmin edilen fiyat y kalite metriği olan evin gerçek fiyatı y ile karşılaştırılarak hata (error) bulunur.” ???
Teşekkürler, elinize sağlık